P与NP及计算的难度：一种规则论的方法
💡
原文英文，约16900词，阅读约需62分钟。
📝
内容提要
本文探讨了计算机科学中的复杂性问题，特别是P与NP问题。尽管理论上难以解决，通过对图灵机的实证研究发现，小程序表现出复杂行为。研究指出某些函数的计算时间存在下限，且计算不可简化。通过比较不同图灵机，揭示了计算不可约性现象，强调了实证方法在理论计算机科学中的重要性。
🎯
关键要点
- 本文探讨计算机科学中的复杂性问题，特别是P与NP问题。
- 通过对图灵机的实证研究发现，小程序表现出复杂行为。
- 某些函数的计算时间存在下限，且计算不可简化。
- 比较不同图灵机揭示了计算不可约性现象。
- 强调实证方法在理论计算机科学中的重要性。
- 使用图灵机模型来枚举可能的程序。
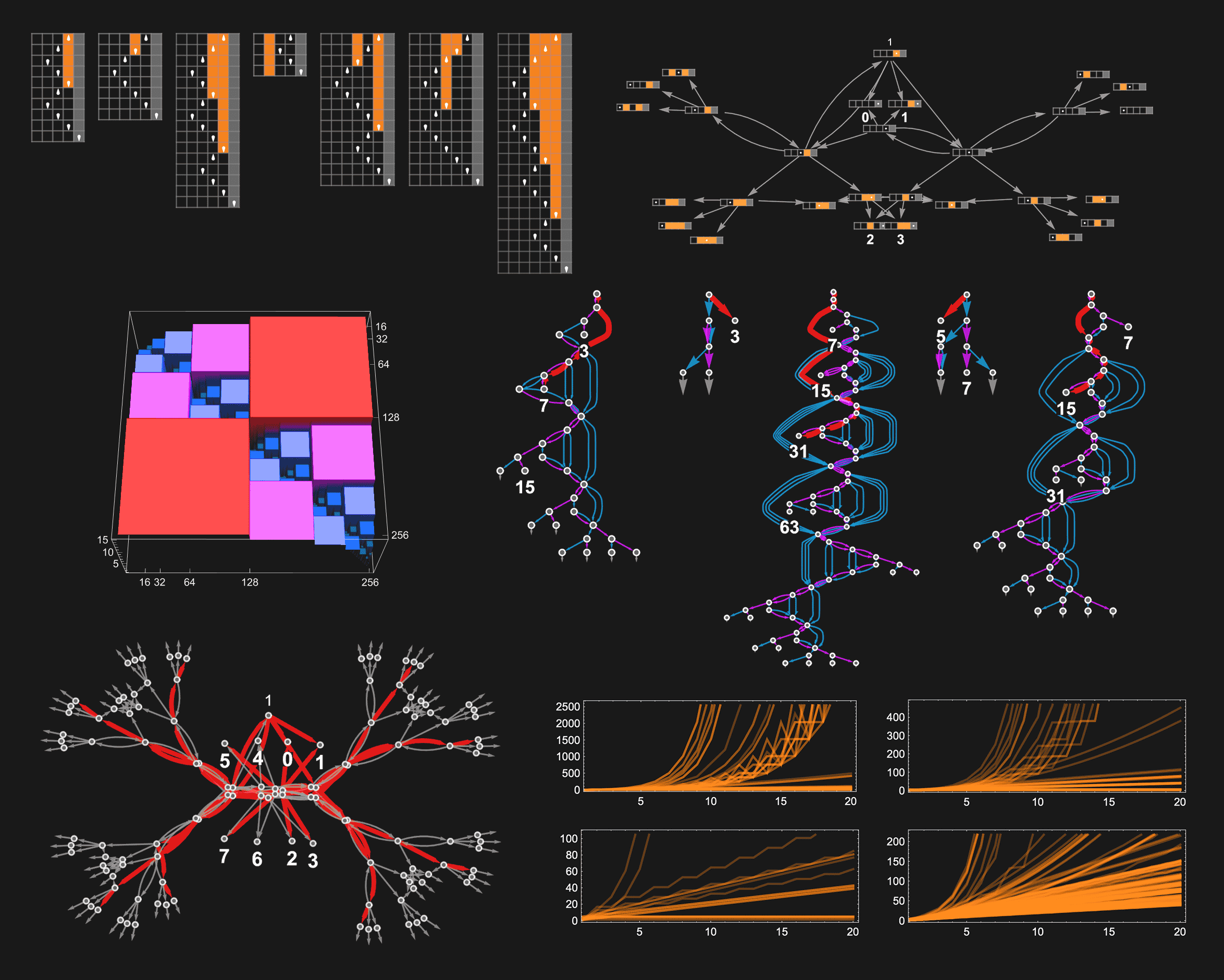
- 研究不同图灵机计算整数函数的表现。
- 探讨了计算复杂性理论中的基本问题和细微差别。
- 通过实证方法获得了计算不可约性的证据。
- 分析了不同状态和颜色的图灵机的计算能力。
- 讨论了计算时间的分布和最坏情况的运行时间。
- 探讨了如何通过更大的图灵机计算函数的速度。
- 总结了s=3, k=2图灵机的计算函数及其运行时间特征。
- 发现某些函数的计算时间下限是指数级的。
- 探讨了不同图灵机在计算相同函数时的速度比较。
➡️
