
德国电商平台OTTO首次向部分欧盟国家开放入驻渠道
Jing Blog
·

不用学 ai
happy xiao 的博客
·

日本:红枫季的关东与关西(关东篇)
少数派
·

县城年轻人,看不起春节电影
TechWeb 全站精华
·

Xbox掌门人斯宾塞宣布退休:微软游戏,也要洗牌了
Jing Blog
·
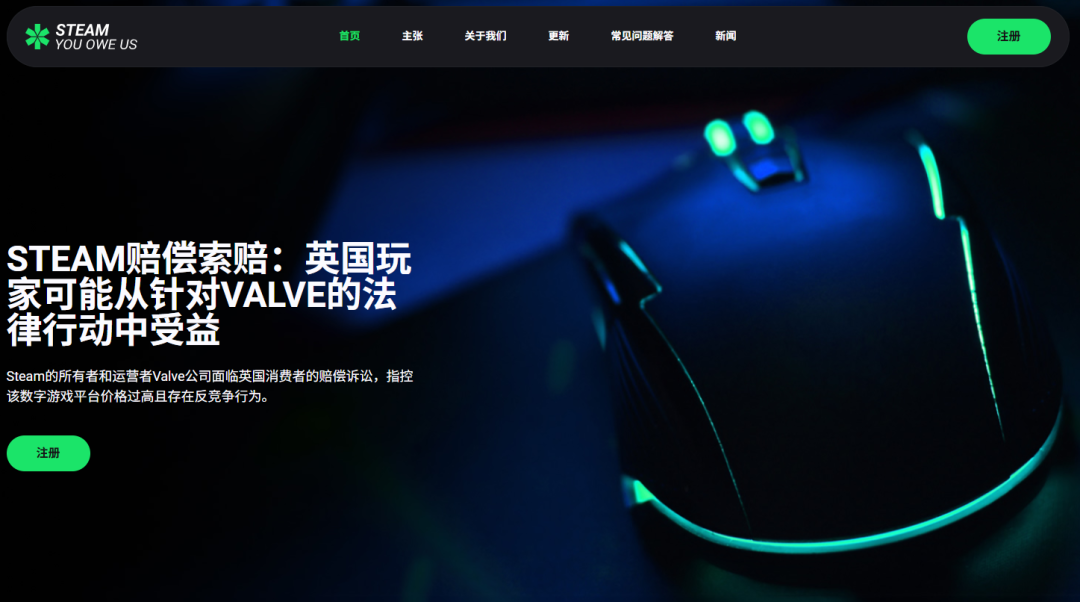
1400万玩家起诉,60亿赔金,能否叫停Steam“三七分账”?
Jing Blog
·
我们是如何构建Agent Builder的内存系统的
LangChain Blog
·
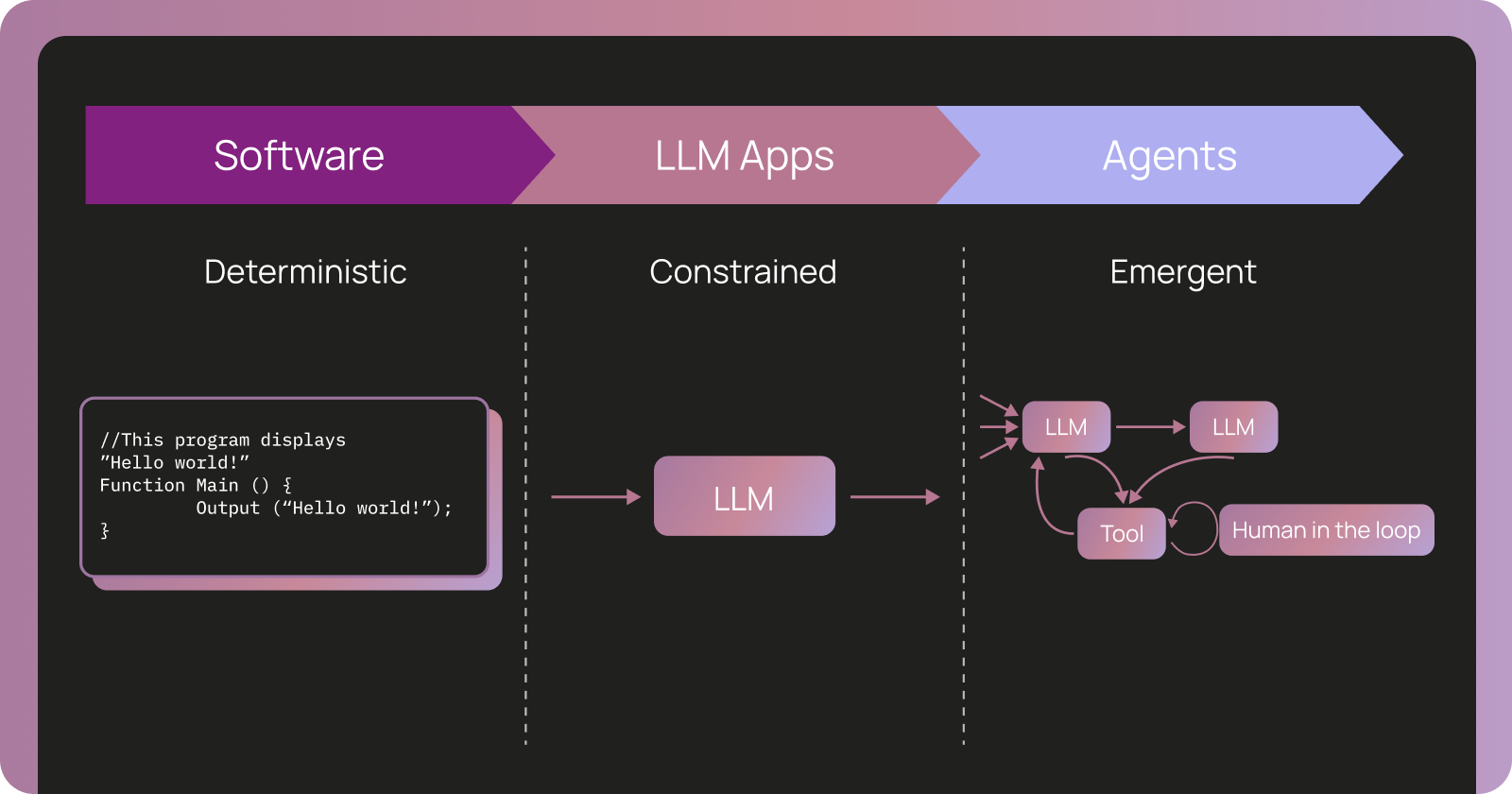
代理可观察性推动代理评估
LangChain Blog
·



![[附临时解决办法] OpenClaw 2026.2.19-2版存在故障 升级后配对状态会失效](https://img.lancdn.com/landian/2026/02/111869.png)


